Question

A 25-mm-diameter uniform steel shaft is 600 mm long between bearings.

a) Find the lowest critical speed of the shaft.
b) If the goal is to double the critical speed, find the new diameter.
c) A half-size model of the original shaft has what critical speed.

Answer 1

a) the lowest critical speed of the shaft is 880.57 rad/s

b) the new diameter when the critical speed is doubled is 0.05 m

c) the critical speed is 1761.14 rad/s and is doubled.

Step-by-step explanation:

a) The moment of inertia is:

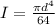`I=(\pi d^(4) )/(64)` (eq. 1)

The area is:

`A=(\pi d^(2) )/(4)`

The speed of the shaft is:

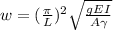`w=((\pi )/(L) )^(2) \sqrt{(gEI)/(A\gamma ) }` (eq. 3)

Where

γ = weight density of the material = 76.5 kN/m³

E = modulus of elasticity = 207x10⁶kN/m²

L = length of the shaft = 0.6 m

d = 0.025 m

Replacing eq. 1, eq. 2 in eq. 3:

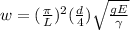`w=((\pi )/(L) )^(2) ((d)/(4) )\sqrt{(gE)/(\gamma ) }` (eq. 4)

`w=((\pi )/(0.6) )^(2) ((0.025)/(4) )\sqrt{(9.8*207x10^(6) )/(76.5) } =880.57rad/s`

b) The diameter of the shaft when the critical speed is doubled is equal to:

`2w=((\pi )/(L) )^(2) ((d)/(4) )\sqrt{(gE)/(\gamma ) }\\d=(4L^(2)*2w )/(\pi ^(2) ) \sqrt{(\gamma )/(gE) } \\d=(4*0.6^(2)*2*880.57 )/(\pi ^(2) ) \sqrt{(76.5)/(9.8*207x10^(6) ) }=0.05m`

c) Transforming equation 4 into:

`(L^(2)w )/(d) =((\pi ^(2) )/(4) )\sqrt{(gE)/(\gamma ) }\\\sqrt{(gE)/(\gamma ) }is-constant\\(L_(1) ^(2)w_(1) )/(d_(1) )=(L_(2) ^(2)w_(2) )/(d_(2) )`

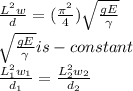
If: L₂ = L/2 and d₂ = d/2, then:

`(L ^(2)w )/(d )=((w_(2)((L)/(2))^(2) )/((d)/(2) ) )\\w_(2) =2w`

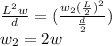
Replacing:

w₂ = 2 * 880.57 = 1761.14 rad/s

The critical speed is doubled.