Answer:
The probability that their mean life will be longer than 13 years = .9943 or 99.43%
Explanation:
Given -
Mean
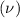 = 15 years
= 15 years
Standard deviation
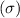 = 3.7 years
= 3.7 years
Sample size ( n ) =22
Let
 be the mean life of manufacturing items
be the mean life of manufacturing items
the probability that their mean life will be longer than 13 years =
 =
=
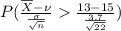
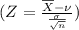
=
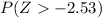
=
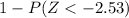 Using Z table
Using Z table
= 1 - .0057
= .9943