Question

You stand on a straight desert road at night and observe a vehicle approaching. This vehicle is equipped with two small headlights that are 0.673 m 0.673 m apart. At what distance, in kilometers, are you marginally able to discern that there are two headlights rather than a single light source? Take the wavelength of the light to be 543 nm 543 nm and your pupil diameter to be 5.37 mm.

Answer 1

To solve this problem we will apply trigonometric and optical concepts that allow us to obtain the minimum distance required. The resolution of the eye is given under the following condition,

`\theta = (1.22\lambda)/(D)`

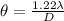
Here,

`\lambda = Wavelength`

`D = Diameter`

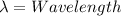
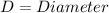
With the values we have that the diameter will be,

`\theta = (1.22(534nm))/(5.37mm)`

`\theta = 1.213*10^(-4)`

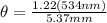
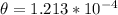
The relation between the distance of the lights and the distance from the eye to the lamp is given under the function,

`sin\theta = (d)/(L)`

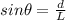
For small angles
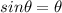`sin\theta = \theta`, then

`\theta = (d)/(L)`

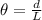
Here,

d = Distance between lights

L = Distance from eye to lamp

`1.213*10^(-4) = (0.673m)/(L)`

`L = (0.673m)/(1.213*10^(-4))`

`L = 5548.22m`

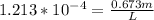
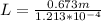
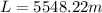
Therefore the distance will be 5.5km