Question

In a two-slit experiment, the slit separation is 3.0 × 10-5 m. The interference pattern is created on a screen that is 2.0 m away from the slits. If the seventh bright fringe on the screen is a linear distance of 10.0 cm away from the central fringe, what is the wavelength of the light?

Answer 1

To solve the problem we will apply the concepts related to the two slit experiment which describes the slit separation by the angle of projection as a function of the order of the bright fringe by the wavelength, this can be mathematically described as,

`dsin\theta = m\lambda`

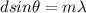
Here,

d = Slit separation

`\lambda` = Wavelength

m = Order of bright fringe

At the same time the distance of the central spot is defined as,

`y = (m \lambda R)/(d)`

Here,

`\lambda`= Wavelength

R = Distance from slit to screen

Using the latest equation and rearranging to find the wavelength, we have,

`\lambda = (yd)/(mR)`

`\lambda = (0.1*3^(-5))/(7*2)`

`\lambda = 214.2nm`

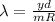
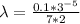
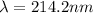
Therefore the wavelenght of the light is 214.2nm