Question

Two astronauts are floating together with zero speed in a gravity-free region of space. The mass of astronaut A is 110 kg and that of astronaut B is 74 kg. Astronaut A pushes B away, with B attaining a final speed of 0.4. The final recoil speed of astronaut A is:

Answer 1

The recoil speed of Astronaut A is 0.26 m/s.

Step-by-step explanation:

Given that,

Mass of astronaut A,
`m_A=110\ kg`

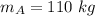
Mass of astronaut B,
`m_B=74\ kg`

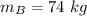
Astronaut A pushes B away, with B attaining a final speed of 0.4,
`v_B=0.4\ m/s`

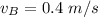
We need to find the recoil speed of astronaut A. The momentum remains conserved here. Using the law of conservation of linear momentum as :

`m_Av_A=m_Bv_B\\\\v_A=(m_Bv_B)/(m_A)\\\\v_A=(74* 0.4)/(110)\\\\v_A=0.26\ m/s`

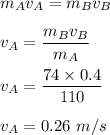
So, the recoil speed of Astronaut A is 0.26 m/s.