Question

A small bulb is rated at 7.5 W when operated at 125 V. The tungsten filament has a temperature coefficient of resistivity α = 0.0045/°C. When the filament is hot and glowing, its temperature is seven times room temperature (20 °C). What is the resistance of the filament (in ohms) at room temperature? Group of answer choices 1911 1350 1280 5630 4530

Answer 1

To solve this problem we will apply the concepts related to resistance as a function of temperature, product of the relationship between the squared voltage and the power. Mathematically this is,

`R = (v^2)/(P)`

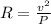
Here,

R = Resistance (At function of temperature)

v = Voltage

P = Power

Then we have,

R at 140°C (7 times room temperature),

`R(140\°C) = (125^2)/(7.5)`

`R(140\°C) = 2083.33\Omega`

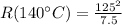
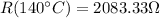
The relationship between normal temperature and increased temperature would then be given by,

`R(140\°C) = R(20\°C)(1 +\alpha (\Delta T))`

`R(140\°C) = R(20\°C)(1+(4.5*10^(-3))(140-20))`

`R(20\°C) = (2083.33)/(1.54)`

`R(20\°C) = 1352.81\Omega`

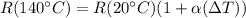
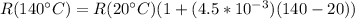
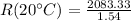
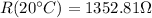
Therefore the correct value of the group of answer is 1350