Question

You calculate the Wilson equation parameters for the ethanol (1) 1 1-propanol (2) system at 258C and find they are L12 5 0.7 and L21 5 1.1. Estimate the value of the parameters at 508C

Answer 1

Here is the correct question.

You calculate the Wilson equation parameters for the ethanol (1) +1 - propanol (2) system at 25° C and find they are ∧₁₂ = 0.7 and ∧₂₁ = 1.1 . Estimate the value of parameters at 50° C

Answer:

the values of the parameters at 50° C are 0.766 and 1.047

Step-by-step explanation:

From "critical point , enthalpy of phase change and liquid molar volume " the liquid molar volume (v) of ethanol and 1 - propanol is represented as follows:

Compound Liquid molar volume (cm³/mol)

Ethanol (1) 58.68

1 - propanol (2) 75.14

To calculate the temperature dependent parameters of the Wilson equation ∧₁₂.

∧₁₂ =
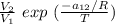`(V_2)/(V_1) \ exp \ ((-a_(12)/R)/(T) )` ------------ equation (1)

where:

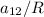`a_(12)/R` = Wilson parameter = ???

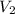`V_2` = liquid molar volume of component 2 = 75.14 cm³/mol

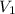`V_1` = liquid molar volume of component 1 = 58.68 cm³/mol

T = temperature = 25° C = ( 25 + 273.15) K = 298.15 K

Replacing our values in the above equation ; we have:

`0.7 = (75.14 \ cm^3/mol)/(58.68 \ cm^3/mol) \ exp \ ((-a_(12)/R)/(298.15 \ K) )`

`0.7 = 1.281 \ exp \ ((-a_(12)/R)/(298.15 \ K) )`

`In (0.547) = \ ((-a_(12)/R)/(298.15 \ K) )`

`-a_(12)/R= 0.60 * 298.15 \ K`

`-a_(12)/R= - 178.89 \ K`

`a_(12)/R= 178.89 \ K`

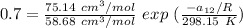
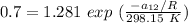
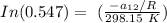
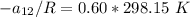
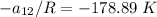
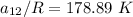
To calculate the temperature dependent parameters of the Wilson equation ∧₂₁

∧₂₁ =
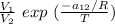`(V_1)/(V_2) \ exp \ ((-a_(12)/R)/(T) )` ---------- equation (2)

`1.1 = (58.68 \ cm^3/mol)/(75.14 \ cm^3/mol) \ exp \ ((-a_(12)/R)/(298.15 \ K) )`

`1.1 = 0.7809 \ exp \ ((-a_(12)/R)/(298.15 \ K) )`

`(1.1)/(0.7809)= exp \ ((-a_(12)/R)/(298.15 \ K) )`

`1n ( 1.4086)= ((-a_(12)/R)/(298.15 \ K) )`

`-a_(12)/R = 0.3426 * 298.15 \ K`

`-a_(12)/R =102.15 \ K`

`a_(12)/R = -102.15 \ K`

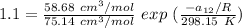
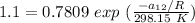
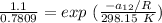
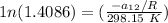
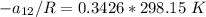
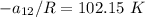
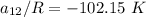
From equation (1) ; let replace 178.98 K for
`a_(12)/R`

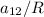
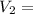`V_2 =` 75.14 cm³/mol

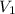`V_1` = 58.68 cm³/mol

T = 50° C = ( 50 + 273.15 ) K = 348.15 K

So;

∧₁₂ =
`(75.14 \ cm^3/mol)/(58.68 \ cm^3/mol) \ exp \ ((- 178,.89 \ K)/(348.15 \ K) )`

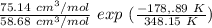
∧₁₂ = 1.281 exp(-0.5138)

∧₁₂ = 1.281 × 0.5982

∧₁₂ =0.766

From equation 2; let replace 102.15 K for
`a_(12)/R`

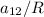
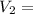`V_2 =` 75.14 cm³/mol

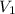`V_1` = 58.68 cm³/mol

T = 50° C = ( 50 + 273.15 ) K = 348.15 K

So;

∧₂₁ =
`(58.68 \ cm^3/mol)/(75.14 \ cm^3/mol) \ exp \ ((-(-102.15)\ K)/(298.15 \ K) )`

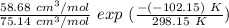
∧₂₁ = 0.7809 exp (0.2934)

∧₂₁ = 0.7809 × 1.3410

∧₂₁ = 1.047

Thus, the values of the parameters at 50° C are 0.766 and 1.047