Question

A survey on British Social Attitudes asked respondents if they had ever boycotted goods for ethical reasons (Statesman, January 28, 2008). The survey found that 23% of the respondents have boycotted goods for ethical reasons. a) In a sample of six British citizens, what is the probability that two have ever boycotted goods for ethical reasons? b) In a sample of six British citizens, what is the probability that at least two respondents have boycotted goods for ethical reasons? c) In a sample of ten British citizens, what is the probability that between 3 and 6 have boycotted goods for ethical reasons? d) In a sample of ten British citizens, what is the expected number of people that have boycotted goods for ethical reasons? Also find the standard deviation.

Answer 1

a) 27.89% probability that two have ever boycotted goods for ethical reasons

b) 41.81% probability that at least two respondents have boycotted goods for ethical reasons

c) 41.16% probability that between 3 and 6 have boycotted goods for ethical reasons

d) The expected number is 2.3 and the standard deviation is 1.33.

Explanation:

We use the binomial probability distribution to solve this question.

Binomial probability distribution

The binomial probability is the probability of exactly x successes on n repeated trials, and X can only have two outcomes.

`P(X = x) = C_(n,x).p^(x).(1-p)^(n-x)`

In which
`C_(n,x)` is the number of different combinations of x objects from a set of n elements, given by the following formula.

`C_(n,x) = (n!)/(x!(n-x)!)`

And p is the probability of X happening.

23% of the respondents have boycotted goods for ethical reasons.

This means that
`p = 0.23`

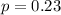
a) In a sample of six British citizens, what is the probability that two have ever boycotted goods for ethical reasons?

This is P(X = 2) when n = 6. So

`P(X = x) = C_(n,x).p^(x).(1-p)^(n-x)`

`P(X = 2) = C_(6,2).(0.23)^(2).(0.77)^(4) = 0.2789`

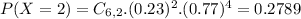
27.89% probability that two have ever boycotted goods for ethical reasons

b) In a sample of six British citizens, what is the probability that at least two respondents have boycotted goods for ethical reasons?

Either less than two have, or at least two. The sum of the probabilities of these events is decimal 1. So

`P(X < 2) + P(X \geq 2) = 1`

`P(X \geq 2) = 1 - P(X < 2)`

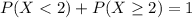
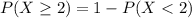
In which

`P(X < 2) = P(X = 0) + P(X = 1)`

`P(X = 0) = C_(6,0).(0.23)^(0).(0.77)^(6) = 0.2084`

`P(X = 1) = C_(6,1).(0.23)^(1).(0.77)^(5) = 0.3735`

`P(X < 2) = P(X = 0) + P(X = 1) = 0.2084 + 0.3735 = 0.5819`

`P(X \geq 2) = 1 - P(X < 2) = 1 - 0.5819 = 0.4181`

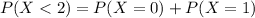
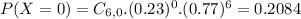
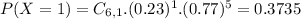
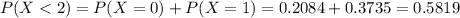
41.81% probability that at least two respondents have boycotted goods for ethical reasons

c) In a sample of ten British citizens, what is the probability that between 3 and 6 have boycotted goods for ethical reasons?

Now n = 10.

`P(3 \leq X \leq 6) = P(X = 3) + P(X = 4) + P(X = 5) + P(X = 6)`

`P(X = 3) = C_(10,3).(0.23)^(3).(0.77)^(7) = 0.2343`

`P(X = 4) = C_(10,4).(0.23)^(4).(0.77)^(6) = 0.1225`

`P(X = 5) = C_(10,5).(0.23)^(5).(0.77)^(5) = 0.0439`

`P(X = 6) = C_(10,6).(0.23)^(6).(0.77)^(4) = 0.0109`

`P(3 \leq X \leq 6) = P(X = 3) + P(X = 4) + P(X = 5) + P(X = 6) = 0.2343 + 0.1225 + 0.0439 + 0.0109 = 0.4116`

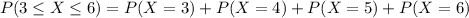
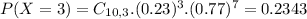
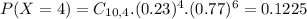
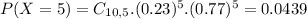
41.16% probability that between 3 and 6 have boycotted goods for ethical reasons

d) In a sample of ten British citizens, what is the expected number of people that have boycotted goods for ethical reasons? Also find the standard deviation.

`E(X) = np = 10*0.23 = 2.3`

`√(V(X)) = √(np(1-p)) = √(10*0.23*0.77) = 1.33`

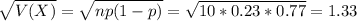
The expected number is 2.3 and the standard deviation is 1.33.