Answer:
56 hours 25 minutes
Explanation:
Given:
Suppose it takes 45 hours for robot A to construct a new robot
It takes 25 hours for both robots to construct a new robot.
Question asked:
How long would it take robot B to construct a new robot, working alone ?
Solution:
Let the time taken by robot B to construct new robot =

By robot A
It takes 45 hours to construct = 1 new robot
It takes 1 hour to construct =
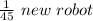
By robot B
It takes
 hours to construct = 1 new robot
hours to construct = 1 new robot
It takes 1 hour to construct =
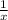 new robot
new robot
By working together
It takes 25 hours to construct = 1 new robot
It takes 1 hour to construct =
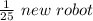
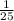 new robot is constructed in = 1 hour
new robot is constructed in = 1 hour
New robot is constructed by both working together in 1 hour = New robot is constructed by robot A in 1 hour + New robot is constructed by robot B in 1 hour
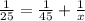
Subtracting both sides by
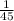
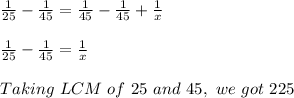
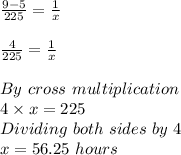
Thus, robot B would take 56 hours 25 minutes to construct a new robot, working alone.