Question

Two hypothetical planets of masses m1 and m2 and radii r1 and r 2 , respectively, are nearly at rest when they are an infinite distance apart. Because of their gravitational attraction, they head toward each other on a collision course. (a) When their center-to-center separation is d, find expressions for the speed of each planet and their relative velocity. (b) Find the kinetic energy of each planet just before they collide, if m1 2.00 1024 kg, m2 8.00 1024 kg, r1 3.00 106 m, and r 2 5.00 106 m. (Hint: Both energy and momentum are conserved.)

Answer 1

(a)
`v_1 = m_2\sqrt{(2G)/(d(m_1+m_2)) }`

`v_2=m_1\sqrt{(2G)/(d(m_1+m_2)) }`

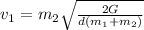
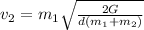
(b) Kinetic Energy of planet with mass m₁, is KE₁ = 1.068×10³² J

Kinetic Energy of planet with mass m₂, KE₂ = 2.6696×10³¹ J

Step-by-step explanation:

Here we have when their distance is d apart

`F_(1) = F_(2) =G(m_(1)m_(2))/(d^(2))`

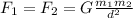
Energy is given by

`Energy \,of \,attraction = -G(m_(1)m_(2))/(d)}+(1)/(2) m_(1) v^2_1+ (1)/(2) m_(2) v^2_2`

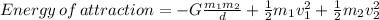
Conservation of linear momentum gives

m₁·v₁ = m₂·v₂

From which

v₂ = m₁·v₁/m₂

At equilibrium, we have;

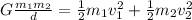`G(m_(1)m_(2))/(d)} = (1)/(2) m_(1) v^2_1+ (1)/(2) m_(2) v^2_2` which gives

`2G{m_(1)m_(2)}= d m_(1) v^2_1+ dm_(2) ((m_1)/(m_2)v_1)^2= dv^2_1(m_1+((m_1)/(m_2) )^2)`

multiplying both sides by m₂/m₁, we have

`2Gm^2_(2)}= dv^2_1 m_2+dm_1v^2_1 =dv^2_1( m_2+m_1)`

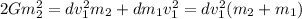
Such that v₁ =
`\sqrt{(2Gm^2_2)/(d(m_1+m_2)) }`

`v_1 = m_2\sqrt{(2G)/(d(m_1+m_2)) }`

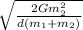
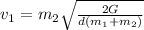
Similarly, with v₁ = m₂·v₂/m₁, we have

`G(m_(1)m_(2))/(d)} = (1)/(2) m_(1) v^2_1+ (1)/(2) m_(2) v^2_2\Rightarrow 2G{m_(1)m_(2)}= dm_(1) ((m_2)/(m_1)v_1)^2 +d m_(2) v^2_2= dv^2_2(m_2+((m_2)/(m_1) )^2)`

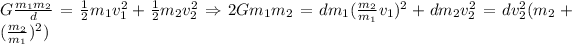
From which we have;

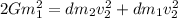`2G{m^2_(1)}= dm_(2) v_2^2 +d m_(1) v^2_2` and

`v_2=m_1\sqrt{(2G)/(d(m_1+m_2)) }`

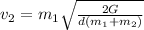
The relative velocity = v₁ + v₂ =
`v_1+v_2=m_1\sqrt{(2G)/(d(m_1+m_2)) } + m_2\sqrt{(2G)/(d(m_1+m_2)) } = (m_1+m_2)\sqrt{(2G)/(d(m_1+m_2)) }`

v₁ + v₂ =
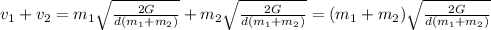
`(m_1+m_2)\sqrt{(2G)/(d(m_1+m_2)) }`

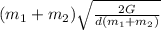
(b) The kinetic energy KE =
`(1)/(2)mv^2`

`KE_1= (1)/(2) m_(1) v^2_1 \, \, \, KE_2= (1)/(2) m_(2) v^2_2`

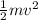
Just before they collide, d = r₁ + r₂ = 3×10⁶+5×10⁶ = 8×10⁶ m

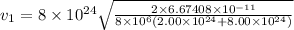`v_1 = 8*10^(24)\sqrt{\frac{2*6.67408 * 10^(-11)} {8*10^6(2.00*10^(24)+8.00*10^(24))} }` = 10333.696 m/s

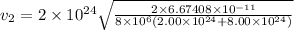`v_2 = 2*10^(24)\sqrt{\frac{2*6.67408 * 10^(-11)} {8*10^6(2.00*10^(24)+8.00*10^(24))} }` =2583.424 m/s

KE₁ = 0.5×2.0×10²⁴× 10333.696² = 1.068×10³² J

KE₂ = 0.5×8.0×10²⁴× 2583.424² = 2.6696×10³¹ J.