Answer:
The induced emf between two end is
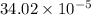 V
V
Step-by-step explanation:
Given:
Length of rod
 m
m
Height
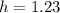 m
m
Magnetic field
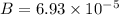 T
T
For finding induced emf,
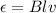
Where
 velocity of rod,
velocity of rod,
For finding the velocity of rod.
From kinematics equation,
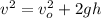
Where
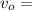 initial velocity,
initial velocity,
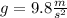
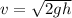
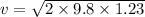
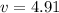

Put the velocity in above equation,
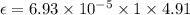
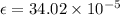 V
V
Therefore, the induced emf between two end is
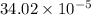 V
V