Answer: p = 6, r = 3 or p = -1, r = -1/2
Explanation:
Since p - 3, p + 3, and 4p + 3 are consecutive terms in a geometric progression, then the proportion of the 2nd term over the 1st equals the 3rd term over the 2nd term.
Step 1 is to find p.
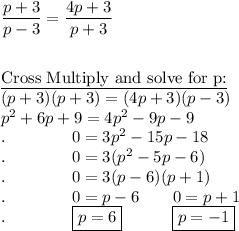
I will show that 3 is not valid below
Step 2 is to find r (common ratio).
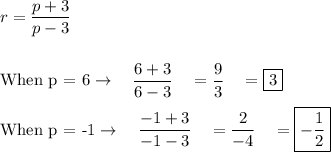
Check:
p = 6 p = -1
p - 3: 6 - 3 = 3 -1 - 3 = -4
p + 3: 6 + 3 = 9 -1 + 3 = 2
4p + 3: 4(6) + 3 = 27 4(-1) + 3 = -1
3(3) = 9
 -4(-1/2) = 2
-4(-1/2) = 2
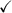
9(3) = 27
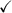 2(-1/2) = -1
2(-1/2) = -1