Answer:
The maximum height is 25 feet
Explanation:
The correct question is
The function h(t)=-16t^2+40t models the height in feet of a ball t seconds after it is thrown into the air. What is the maximum height the ball reaches after it is thrown?
we have
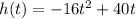
This is a vertical parabola open downward (the leading coefficient is negative)
The vertex represent a maximum
The y-coordinate of the vertex represent the maximum height that the ball reaches
Convert the quadratic equation in vertex form
Factor -16
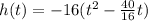
simplify
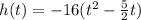
Complete the square
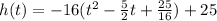
Rewrite as perfect squares
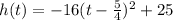
The vertex is the point (1.25,25)
therefore
The maximum height is 25 feet