Question

In triangle ABC, mA= 40°, the length of side AB is 7 cm and the length of side BC is 5 cm. Find the measure of angle C using the law of sines.​

Answer 1

The answer is 64.15

Answer 2

C = 64.145º

Explanation:

The Law of Sines is as follows:

`(sinA)/(a)` =
`(sinB)/(b)` =
`(sinC)/(c)`

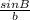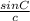
The problem can be draw as the picture attached.

Now, the values of the sides and angles can be substituted into the Law of Sines, and because all parts are equal, only two are needed:

`(sin40)/(5)` =
`(sinC)/(7)`

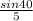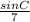
Next, cross-multiply:

7sin40º = 5sinC

Then, divide both sides by 5:

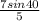`(7sin40)/(5)` = sinC

Finally, take the inverse sin of the left side and convert into a decimal:

C =
`sin^(-1)`(
`(7sin40)/(5)`)

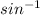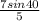C = 64.145