Question

A 20.0 kg crate sits at rest at the bottom of a 15.0-m-long ramp that is inclined at 34.0° above horizontal. A constant horizontal force of 290 N is applied to the crate to push it up the ramp. While the crate is moving, the ramp exerts a constant frictional force on it that has magnitude 65.0 N.

(A) Is the total work done on the crate during its motion from the bottom to the top of the ramp?
Express your answer to three significant figures and include the appropriate units.
(B) How much time does it take the crate to travel to the top of the ramp?
Express your answer to three significant figures and include the appropriate units.

Answer 1

To calculate the total work done on the crate, we must account for the work by both the applied horizontal force and the frictional force. Then we can determine the time taken for the crate to reach the top of the ramp using Newton's second law and kinematics.

Step-by-step explanation:

The student's schoolwork question deals with the concept of work done by forces when moving an object up an inclined plane, and it also involves finding the time taken for this movement. According to physics, work is defined as the product of the force and the displacement in the direction of the force. For part (A), we need to calculate the total work done on a 20.0 kg crate by summing up the work done by the applied horizontal force and the work done against friction. The work done by the horizontal force is the product of the force, the displacement along the ramp, and the cosine of the angle between the force and displacement. Since the ramp's length is given and the force is horizontal, the displacement in the direction of the force is 15.0 m times the cosine of 34.0°.

For part (B), determining the time taken for the object to reach the top of the ramp requires knowing the acceleration of the crate and the distance traveled. Newton's second law can help us find acceleration, knowing the net force and the mass. Once we have acceleration, we can use kinematics equations to find the time.

Answer 2

987 joules, 3.01s

Step-by-step explanation:

(A)

from the attached diagram

net force, Fnet, pulling the crate up the ramp is given by

Fnet = FcosФ - WsinФ - Fr

where FcosФ is the component of horizontal force 290N resolved parallel to the plane

WsinФ = mgsinФ = component of the weight of the crate resolved parallel to the plane

Fr = constant opposing frictional force

Fnet = 290cos34⁰ - 20 × 9.8 × sin34° - 65

Fnet = 240.421 - 109.602 - 65

Fnet = 65.82N

Work done on the crate up the ramp, W, is given by

W = Fnet × d (distance up the plane)

W = 65.819 × 15

W = 987.285 joules

W = 987 joules (to 3 significant Figures)

(B)

to calculate the time of travel up the ramp

we use the equation of motion

`s = ut + (1)/(2)at^(2)`

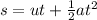
where s = distance up the plane, 15m

u = Initial velocity of the crate, which is 0 for a body that is initially at rest

a = acceleration up the plane, given by

`a = (Fnet)/(m)`

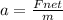
where m = mass of the crate, 20 kg

now,
`a = (65.819)/(20) \\a = 3.291(m^(2) )/(s)`

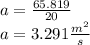
from,
`s = ut + (1)/(2)at^(2)`

`15 = 0*t + (1)/(2)* 3.291 * t^(2)`

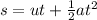
15 = 0 + 1.645
`t^(2)`

15 = 1.645
`t^(2)`

`t = \sqrt{(15)/(1.645) }`

`t = 3.019`

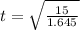
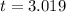
t = 3.01s (to 3 sig fig)