Answer:
987 joules, 3.01s
Step-by-step explanation:
(A)
from the attached diagram
net force, Fnet, pulling the crate up the ramp is given by
Fnet = FcosФ - WsinФ - Fr
where FcosФ is the component of horizontal force 290N resolved parallel to the plane
WsinФ = mgsinФ = component of the weight of the crate resolved parallel to the plane
Fr = constant opposing frictional force
Fnet = 290cos34⁰ - 20 × 9.8 × sin34° - 65
Fnet = 240.421 - 109.602 - 65
Fnet = 65.82N
Work done on the crate up the ramp, W, is given by
W = Fnet × d (distance up the plane)
W = 65.819 × 15
W = 987.285 joules
W = 987 joules (to 3 significant Figures)
(B)
to calculate the time of travel up the ramp
we use the equation of motion
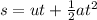
where s = distance up the plane, 15m
u = Initial velocity of the crate, which is 0 for a body that is initially at rest
a = acceleration up the plane, given by
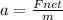
where m = mass of the crate, 20 kg
now,
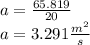
from,
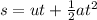
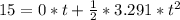
15 = 0 + 1.645
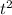
15 = 1.645
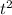
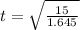
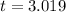
t = 3.01s (to 3 sig fig)