Question

A 0.50-kg object moves on a horizontal frictionless circular track with a radius of 2.5 m. An external force of 3.0 N, always tangent to the track, causes the object to speed up as it goes around. If it starts from rest, then at the end of one revolution the radial component of the force of the track on it is ____________.

Answer 1

Radial force component of force = 37.68 N

Step-by-step explanation:

By Newton's 2 nd law of motion,

F = ma

F = 3.0 N, m = 0.5 Kg, a (Linear Acceleration ) = ?

3 = 0.5 a

a = 6
`m/sec^(2)`

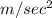
Now, a = 6
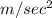`m/sec^(2)` , r = 2.5 m ,α(angular acceleration ) = ?

a = r α

6= 2.5 α

hence α = 2.4 rad/
`sec^(2)`

`w= ?, w_0= 0, \alpha =2.4\ rad/sec^(2),\theta =2\ \pi (One\ Revolution)`

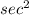
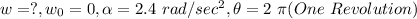
we know that,

`w^(2) =w_0^2 +2 \alpha\cdot s\\ =0 + 2\cdot 2.4\cdot 2\pi\\=30.14 \\w=√(30.144) = 5.49\ Rad/ sec`

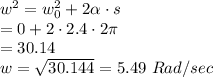
Radial force component of force =
`m r w^(2)`

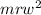
since m =0.5 kg, r =2.5 m w =5.49 rad/sec

Radial force component of force =
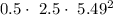`0.5\cdot\ 2.5\cdot\ 5.49^(2)` = 37.68 N