Question

A 0.80-μm-diameter oil droplet is observed between two parallel electrodes spaced 11 mm apart. The droplet hangs motionless if the upper electrode is 22.8 V more positive than the lower electrode. The density of the oil is 885 kg/m^3.

(a) What is the droplet's mass?
(b) What is the droplet's charge?
(c) Does the droplet have a surplus or a deficit of electrons? How many?

Answer 1

Step-by-step explanation:

Given that,

Diameter of the oil droplet,
`d=0.8\ \mu m`

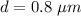
Radius,
`r=0.4\ \mu m=0.4* 10^(-6)\ m`

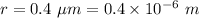
Separation between the electrodes, d = 11 mm

The droplet hangs motionless if the upper electrode is 22.8 V more positive than the lower electrode.

The density of the oil is
`885\ kg/m^3`

(a) Density of oil is given by mas per unit volume.

`d=(m)/(V)\\\\m=d* V\\\\m=d* (4)/(3)\pi r^3\\\\m=885* (4)/(3)\pi (0.4* 10^(-6))^3\\\\m=2.37* 10^(-16)\ kg`

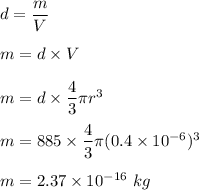
(b) The electric force is balanced by the mass of the object. So,

qE = mg

`q=(mg)/(E)`

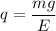
E is electric field, E = V/d

`q=(mgd)/(V)\\\\q=(2.37* 10^(-16)* 9.8* 11* 10^(-3))/(22.8)\\\\q=1.12* 10^(-18)\ C`

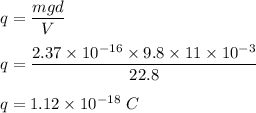
(c) Charges come in integer multiples of the electronic charge units of e. So,

`n=(q)/(e)\\\\n=(1.12* 10^(-18))/(1.6* 10^(-19))\\\\n=7`

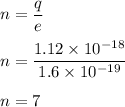
Hence, this is the required solution.