Question

A mining company owns two mines, each of which produces three grades (high, medium, and low) of ore. The company has a contract to supply a smelting company with at least 12 tons of high- grade ore, at least 8 tons of medium-grade ore, and at least 24 tons of low-grade ore. Each hour of operation, mine 1 produces 6 tons of high- grade ore, 2 tons of medium-grade ore, and 4 tons of low-grade ore. Each hour of operation, mine 2 produces 2 tons of high-grade ore, 2 tons of medium-grade ore, and 12 tons of low-grade ore. It costs $200 per hour to operate mine 1 and $160 per hour to operate mine 2. How many hours should each mine be operated so as to meet the contractual obligations at the lowest total operating cost.

Required:
a. Formulate a linear programming model for this problem.
b. Solve this model by using graphical analysis.

Answer 1

They should operate Mine 1 for 1 hour and Mine 2 for 3 hours to meet the contractual obligations and minimize cost.

Step-by-step explanation:

The formulation of the linear programming is:

Objective function:

`C=200M_1+160M_2`

Restrictions:

- High-grade ore:
`6M_1+2M_2\geq12`

- Medium-grade ore:
`2M_1+2M_2\geq8`

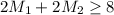
- Low-grade ore:
`4M_1+12M_2\geq24`

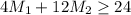
- No negative hours:
`M_1,M_2\geq0`

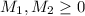
We start graphing the restrictions in a M1-M2 plane.

In the figure attached, we have the feasible region, where all the restrictions are validated, and the four points of intersection of 2 restrictions.

In one of this four points lies the minimum cost.

Graphically, we can graph the cost function over this feasible region, with different cost levels. When the line cost intersects one of the four points with the lowest level of cost, this is the optimum combination.

(NOTE: it is best to start with a low guessing of the cost and going up until it reaches one point in the feasible region).

The solution is for the point (M1=1, M2=3), with a cost of C=$680.

The cost function graph is attached.