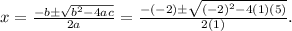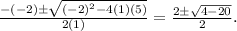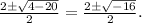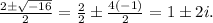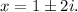1 Answer

Aleks G · Answer 1 · 2021-11-30T15:30:14+0000

For the given equation, the solutions are
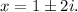
$x = 1 \pm 2i.$

Explanation:

Step 1:

For an equation of the form
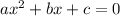ax^(2) +bx+c=0 the solution is
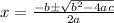$x=\frac{-b \pm \sqrt{b^(2)-4 a c}}{2 a}$ .

Here a is the coefficient of
x^(2) , b is the coefficient of x and c is the constant term.

Comparing
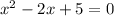x^(2) -2x+5=0 with
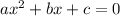ax^(2) +bx+c=0 , we get that a is 1, b is -2 and c is 5.

To get the solution, we substitute the values of a, b, and c in
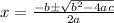$x=\frac{-b \pm \sqrt{b^(2)-4 a c}}{2 a}$ .

Step 2:

Substituting the values, we get

$x=\frac{-b \pm \sqrt{b^(2)-4 a c}}{2 a}=\frac{-(-2) \pm \sqrt{(-2)^(2)-4(1)(5)}}{2(1)}.$

$\frac{-(-2) \pm \sqrt{(-2)^(2)-4(1)(5)}}{2(1)} = (2 \pm √(4-20))/(2).$

$(2 \pm √(4-20))/(2) = (2 \pm √(-16))/(2).$

$(2 \pm √(-16))/(2) = (2)/(2) \pm (4(-1))/(2) = 1 \pm 2i.$

$x = 1 \pm 2i.$

Please log in or register to add a comment.