Question

Let CFG G be the following grammar.

S → aSb | bY | Y a
Y → bY | aY | ε

Give a simple description of L(G) in English. Use that description to give a CFG for L(G), the complement of L(G).

Answer 1

The answer in the explanation section

Step-by-step explanation:

The context free grammar is equal to:

S → aSb|bY|Ya

Y → bY|aY|ε

The language L(G) is equal to:

Y → bY

Y → aY

Y → ε

S → aSb

S → bY

S → Ya

If S → Ya, thus:

S → ∈a

S → a

If S → bY:

S → ∈b

S → b

If S → aSb:

S → abYb

S → abbYb

If S → bY:

S → bbY

S → bb∈

S → bb

From all this cases, the languaje is the follow:

L(G)=[a,b,abbb,bb...]

The description of L(G) is:

-strings made up of a consecutive number of a length a, that can vary from 1 to infinity.

-strings made up of a consecutive number of a length b, that can vary from 1 to infinity.

-strings whose start symbol a is followed by number b

-strings whose start symbol b is followed by number a

-strings beginning with the symbol a and ending with the symbol b

-strings beginning with the symbol b and ending with the symbol a

The grammar for L(G) is equal to
`a^(i) b^(i) if i\geq 0\\`

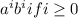
The CFG for L(G) is equal to:

S → aSb|∈

S → abb∈b

S → abbb

Answer 2

See Explanation Below

Step-by-step explanation:

Given

S → aSb | bY | Y a

Y → bY | aY | ε

Giving a simple description of L(G) in English. The description is as follows;

This means that L(G) contains a string of a's and b's such that the following are true;

1. the string starts with n a’s and m b’s, where n and m can be zero, but not at the same time,and at least one of option 2 and option 3

2. and has any number of a’s or b’s followed by an a

3. ab followed by any number of a’s and b’s

Note that n and m represent numerical digits

Using the description to give a CFG for L(G), the complement of L(G) is written as L'(G)

L'G are elements not in L(G) and they are

L'(G) =a^n b (a∪b) * b^n ∪ a^n (a∪b) * ab^n