Question

A 6.60-kg block slides with an initial speed of 1.56 m/s up a ramp inclined at an angle of 28.4° with the horizontal. The coefficient of kinetic friction between the block and the ramp is 0.62.

1. Use energy conservation to find the distance the block slides before coming to rest.

Answer 1

The distance travel by block before coming to rest is 0.122 m

Step-by-step explanation:

Given:

Mass of block
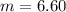`m = 6.60` kg

Initial speed of block
`v _(i) = 1.56`
`(m)/(s)`

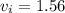
Final speed of block
`v_(f) = 0`
`(m)/(s)`

Coefficient of kinetic friction
`\mu _(k) = 0.62`

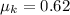
Ramp inclined at angle
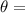`\theta =` 28.4°

Using conservation of energy,

Work done by frictional force is equal to change in energy,

`\mu _(k) mgd \cos 28.4 = \Delta K - \Delta U`

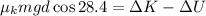
Where
`\Delta U = mg d\sin 28.4`

`\mu _(k) mgd \cos 28.4 = (1)/(2)mv_(i) ^(2) - mgd\sin 28.4`

`\mu _(k) mgd \cos 28.4 +mgd\sin 28.4 = (1)/(2)mv_(i) ^(2)`

`d(6.60 * 9.8 * 0.62 * 0.879 + 6.60 * 9.8 * 0.475) = (1)/(2) * 6.60 * (1.56)^(2)`

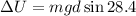
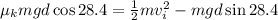
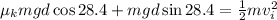
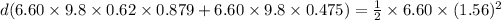
`d = 0.122` m

Therefore, the distance travel by block before coming to rest is 0.122 m