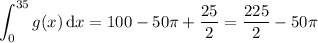(a) The integral is equal to the area of the triangle; it has height 20 and base 10, so the area is 20*10/2 = 100.
(b) The integral is equal to the area of the semicircle with radius 10. It's also under the horizontal axis, so the area is negative. The semicircle has area
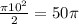 , so the integral is -50π.
, so the integral is -50π.
(c) First compute
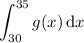
which is the area of the triangle on the right. It has height and base 5, so its area is 25/2.
Then split up the desired integral as
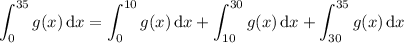
and plug in the integral values you know: