Answer:
The cell voltage of the given cell is 2.01 V
Step-by-step explanation:

Oxidation half reaction:
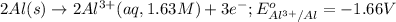
Reduction half reaction:
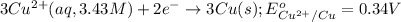
Oxidation reaction occurs at anode and reduction reaction occurs at cathode.
To calculate the
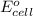 of the reaction, we use the equation:
of the reaction, we use the equation:
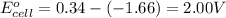
To calculate the EMF of the cell, we use the Nernst equation, which is:
![E_(cell)=E^o_(cell)-(2.303RT)/(nF)\log ([Al^(3+)]^2)/([Cu^(2+)]^3)](https://img.qammunity.org/2021/formulas/chemistry/college/zu2hbxs1z58kumrs45krz1arlkfl6j0c62.png)
where,
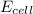 = electrode potential of the cell = ? V
= electrode potential of the cell = ? V
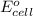 = standard electrode potential of the cell = +2.00 V
= standard electrode potential of the cell = +2.00 V
R = Gas constant = 8.314 J/mol.K
T = temperature =
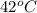 =[42+273]K=315K
=[42+273]K=315K
F = Faraday's constant = 96500
n = number of electrons exchanged = 6
![[Cu^(2+)]=3.43M[Al^(3+)]=1.63M](https://img.qammunity.org/2021/formulas/chemistry/college/pphm6mmjgqmiibiixnvwosmfog7yp2vdtg.png)

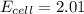
Thus, the cell voltage of the given cell is 2.01