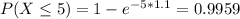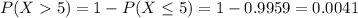1 Answer

Lightstrike · Answer 1 · 2021-07-22T02:50:34+0000

Answer:

a) 0.0821

b) 0.0111

c) 0.0041

Explanation:

Exponential distribution:

The exponential probability distribution, with mean m, is described by the following equation:

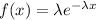
$f(x) = \lambda e^(-\lambda x)$

In which
$\lambda$ is the decay parameter.

The probability that x is lower or equal to a is given by:

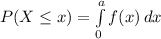
$P(X \leq x) = \int\limits^a_0 {f(x)} \, dx$

Which has the following solution:

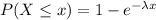
$P(X \leq x) = 1 - e^(-\lambda x)$

Either it lasts more 5 years or less, or it survives more than 5 years. The sum of the probabilities of these events is decimal 1. So

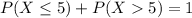
$P(X \leq 5) + P(X > 5) = 1$

In all 3 cases, we want P(X > 5). So

$P(X > 5) = 1 - P(X \leq 5)$

In which

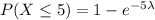
$P(X \leq 5) = 1 - e^(-5\lambda)$

(a) lambda=.5

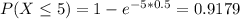
$P(X \leq 5) = 1 - e^(-5*0.5) = 0.9179$

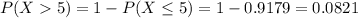
$P(X > 5) = 1 - P(X \leq 5) = 1 - 0.9179 = 0.0821$

(b) lambda=0.9

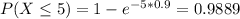
$P(X \leq 5) = 1 - e^(-5*0.9) = 0.9889$

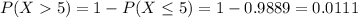
$P(X > 5) = 1 - P(X \leq 5) = 1 - 0.9889 = 0.0111$

(c) lambda=1.1

$P(X \leq 5) = 1 - e^(-5*1.1) = 0.9959$

$P(X > 5) = 1 - P(X \leq 5) = 1 - 0.9959 = 0.0041$

Please log in or register to add a comment.