Question

A gas-turbine power plant operates on the simple Brayton cycle between the pressure limits of 100 and 1600 kPa. The working fluid is air, which enters the compressor at 40°C at a rate of 850 m^3/min and leaves the turbine at 650°C. Using variable specific heats for air and assuming a compressor isentropic efficiency of 85 percent and a turbine isentropic efficiency of 88 percent, determine:

(a) the net power output, (b) the back work ratio, and (c) the thermal efficiency.

Answer 1

(a) The net power output is 6081 kW

(b) The back work ratio is 0.536

(c) The thermal efficiency is 37.4%

Step-by-step explanation:

Process 1-2 is compression

Obtain the properties from EES software.

Enthalpy is function of Temperature for an ideal gas whereas the entropy is a function of both temperature and pressure.

T₁ = 40°C, P₁ = 100 KPa

Enthalpy, h₁ = 313.6 kJ/kg

Enthropy, S₁ = 5.749 kJ/kg.k

Entropy at state 2, s₂ = s₁ = 5.749 kJ/kg.k

P₂ = 1600 kPa and Entropy s₂ = 5.749 kJ/kg.k

Saturated Enthalpy,
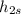`h_(2s)` = 691.9 kJ/kg

The Compressor efficiency is,

`n_c = (h_(2s) -h_1)/(h_2 - h_1)`

`0.85 = (691.9 - 313.6)/(h_2 - 313.6)`

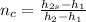
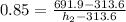
h₂ = 758.6 kJ/kg

Process 3 - 4 is expansion

T₄ = 650°C, specific enthalpy, h₄ = 959.2 kJ/kg

The turbine efficiency is,

`n_t = (h_3 - h_4)/(h_3 - h_(4s))`

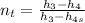
Enthalpy cannot be found directly at state 3.

Using the EES software together with isentropic efficiency relation, we find

Temperature, T₃ = 1353°C

Enthalpy, h₃ = 1790 kJ/kg

Entropy, s₃ = 6.75 kJ/kg.k

Note that: h₃ = enthalpy(Air, T=T₃)

s₃ = entropy(Air, T=T₃, P=P₂)

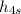`h_(4s)` = enthalpy(Air, P=P₁, s=s₃)

The mass flow rate is determined from

m = P₁V₁ ÷ RT₁

= (100 kPa) (850 m³/min) ÷ (0.287) (40 + 273)

= 15.77 kg/s

The work input to the compressor is:

`W_(c,in) = m (h_2 - h_1)`

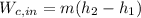
= (15.77 kg/s) (758.6 kJ/kg - 313.6 kJ/kg)

= 7017 kW

The work output from the turbine is:

`W_(T,out) = m (h_3 - h_4)`

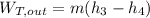
= (15.77 kg/s) ( 1790 kJ/kg - 959.2 kJ/kg)

= 13098 kW

(A) the net power output,

`W_(net) = W_(T, out) - W_(C,in)`

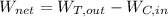
= 13098 kW - 7017 kW

= 6081 kW

(B) The back work ratio is

`r_(bw) = (W_(C, in))/(W_(T, out))`

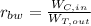
= 7017 kW / 13098 kW

= 0.536

(C) The thermal efficiency is

`n_(th) = (W_(net))/(Q_(in))`

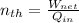
= 6081 kW ÷ [m(h₃ - h₂)]

= 6081 kW ÷ [15.77 kg/s (1790 kJ/kg - 758.6 kJ/kg)]

= 37.4%