Answer:
(a) The impedance in the circuit is
 .
.
(b)The resistance is
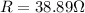 .
.
(c) The inuctance is 0.57 H.
Step-by-step explanation:
(a)
The expression for the impedance is as follows:
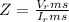
Here,
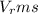 is the rms voltage and
is the rms voltage and
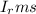 is the rms current.
is the rms current.
Put
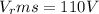 and
and
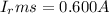 .
.
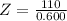

Therefore, the impedance in the circuit is
 .
.
(b)
The expression for the average power is as follows;
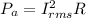
Here,
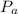 is the average power and R is the resistance.
is the average power and R is the resistance.
Calculate the resistance by rearranging the above expression.

Put
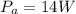 and
and
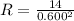
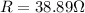
Therefore, the resistance is
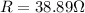 .
.
(c)
The expression for the impedance is as follows;
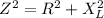
Here,
 is the inductive reactance.
is the inductive reactance.
Put
 and
and
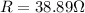 .
.
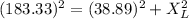
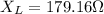
The expression for the inductive reactance in terms of frequency is as follows;
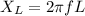
Here, L is the inductance.
Calculate the inductance by rearranging the above expression.
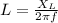
Put
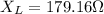 and f=50Hz.
and f=50Hz.
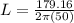
L=0.57 H
Therefore, the inuctance is 0.57 H.