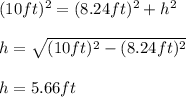Answer:
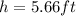
Explanation:
Observe the picture attached.
Find the value of "x" and "y" using the Pythagoren Theorem:
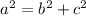
If you solve for "a":
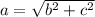
Where "a" is the hypotenuse and "b" and "c" are the legs.
In this case, for "x" you know that:
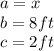
Then, the value of "x" is:
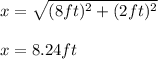
For "y" you can see that:

Subsituting values and solving for h, you get: