Question

An article in Industrial Engineer (September 2012) reported on a study of potential sources of injury to equine veterinarians conducted at a university veterinary hospital. Forces on the hand were measured for several common activities that veterinarians engage in when examining or treating horses. We will consider the forces on the hands for two tasks, lifting and using ultrasound. Assume that both sample sizes are 6, the sample mean force for lifting was 6.0 pounds with standard deviation 1.5 pounds, and the sample mean force for using ultrasound was 6.2 pounds with standard deviation 0.3 pounds (data read from graphs in the article). Assume that the standard deviations are known. Is there evidence to conclude that the two activities result in significantly different forces on the hands?

Answer 1

No, there is no evidence to conclude that the two activities result in significantly different forces on the hands.

Explanation:

We are given that consider the forces on the hands for two tasks, lifting and using ultrasound. Assume that both sample sizes are 6, the sample mean force for lifting was 6.0 pounds with standard deviation 1.5 pounds, and the sample mean force for using ultrasound was 6.2 pounds with standard deviation 0.3 pounds. Assume that the standard deviations are known.

We have to conduct a hypothesis test to determine that the two activities result in significantly different forces on the hands or not.

Let
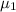`\mu_1` = population mean force for using lifting

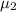`\mu_2` = population mean force for using ultrasound

SO, Null Hypothesis,
`H_0` :
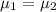`\mu_1 = \mu_2` or
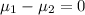`\mu_1-\mu_2=0` {means that the two activities result in significantly same forces on the hands}

Alternate Hypothesis,
`H_a` :
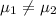`\mu_1\\eq \mu_2` or
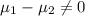`\mu_1-\mu_2 \\eq 0` {means that the two activities result in significantly different forces on the hands}

The test statistics that will be used here is Two-sample z test statistics as we know about the population standard deviations;

T.S. =
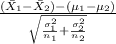`\frac{(\bar X_1 - \bar X_2)-(\mu_1-\mu_2)}{\sqrt{(\sigma_1 ^(2) )/(n_1) +(\sigma_2 ^(2) )/(n_2)} }` ~ N(0,1)

where,
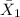`\bar X_1` = sample mean force for using lifting = 6.0 pounds

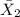`\bar X_2` = sample mean force for using ultrasound = 6.2 pounds

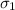`\sigma_1` = standard deviation for using lifting = 1.5 pounds

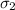`\sigma_2` = standard deviation for using ultrasound = 0.3 pounds

`n_1` = sample size for lifting task = 6

`n_2` = sample size for ultrasound task = 6

So, test statistics =
`\frac{(6.0-6.2)-(0)}{\sqrt{(1.5 ^(2) )/(6) +(0.3 ^(2) )/(6)} }`

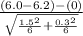
= -0.32

Since in the question we are not given with the significance level so we assume it to be 5%. So, at 0.05 level of significance, the z table gives critical values between -1.96 and 1.96 for two-tailed test. Since our test statistics lies in between the critical values of z so we have insufficient evidence to reject null hypothesis as it will not fall in the rejection region.

Therefore, we conclude that the two activities result in significantly same forces on the hands.