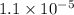Question

The pH of a 0.78M solution of 4-pyridinecarboxylic acid HC6H4NO2is measured to be 2.53.Calculate the acid dissociation constant Ka of 4-pyridinecarboxylic acid. Round your answer to 2 significant digits.

Answer 1

Answer : The value of acid dissociation constant is,
`1.1* 10^(-5)`

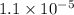
Solution : Given,

Concentration pyridinecarboxylic acid = 0.78 M

pH = 2.53

First we have to calculate the hydrogen ion concentration.

`pH=-\log [H^+]`

`2.53=-\log [H^+]`

`[H^+]=2.95* 106{-3}M`

Now we have to calculate the acid dissociation constant.

The equilibrium reaction for dissociation of (weak acid) is,

`HC_6H_4NO_2\rightleftharpoons C_6H_4NO_2^-+H^+`

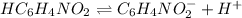
initially conc. 0.78 0 0

At eqm. (0.78-x) x x

The expression of acid dissociation constant for acid is:

`k_a=([C_6H_4NO_2^-][H^+])/([C_6H_4NO_2])`

As,
`[H^+]=[C_6H_4NO_2^-]=x`

So,
`x=2.95* 106{-3}M`

Now put all the given values in this formula ,we get:

`k_a=((x)* (x))/((0.78-x))`

`k_a=\frac{(2.95* 106{-3})* (2.95* 106{-3})}{(0.78-2.95* 106{-3})}`

`K_a=1.1* 10^(-5)`

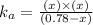
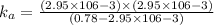
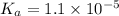
Therefore, the value of acid dissociation constant is,
`1.1* 10^(-5)`