Question

Consider estimating a population proportion p. What is the most conservative sample size (erring on the large size) required in order to build a 95% confidence interval for a population proportion p with a margin of error of at most 2%?

Answer 1

The most conservative sample size is 2401.

Explanation:

We are given the following in the question:

We are not given any approximation of s]ample proportion, thus,

`\hat{p} = 0.5`

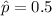
We have to construct a 95% confidence interval.

Margin of error = 2% = 0.02

Formula for margin of error =

`z_(stat)\sqrt{\frac{\hat{p}(1-\hat{p})}{n}}`

`z_(critical)\text{ at}~\alpha_(0.05) = 1.96`

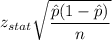
Putting values, we get,

`0.02 = 1.96* \sqrt{\frac{\hat{p}(1-\hat{p})}{n}}\\\\0.02 = 1.96* \sqrt{(0.5(1-0.5))/(n)}\\\\√(n) = 1.96* (√(0.5(1-0.5)))/(0.02)\\\\√(n)=49\\n = 2401`

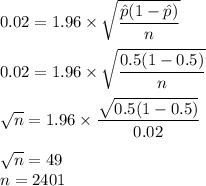
Thus, the most conservative sample size is 2401.