Question

A positive integer is 1 less than another. If the sum of the reciprocal of the smaller and twice the reciprocal of the larger is frac(7,6), then find the two integers

Answer 1

The two integers are 2 and 3.

Explanation:

Let the larger positive integer be 'x'.

Now given:

A positive integer is 1 less than another.

So Smaller integer will be =
`x-1`

We need to find the two integers.

Solution:

Now given:

If the sum of the reciprocal of the smaller and twice the reciprocal of the larger is
`\frac76`

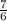
So we can say that;

`(1)/(x-1)+(2)/(x)=\frac76`

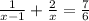
Now we will make the denominator common using LCM.

`(x)/(x(x-1))+(2(x-1))/(x(x-1))=\frac76`

Now denominator are common so we will solve the numerator;

`(x+2x-2)/(x(x-1))=\frac76\\\\(3x-2)/(x(x-1))=\frac76`

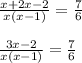
Using cross multiplication we get;

`6(3x-2)=7x(x-1)\\\\18x-12=7x^2-7x\\\\7x^2-7x-18x+12=0\\\\7x^2-25x+12=0`

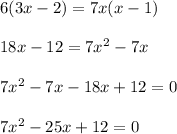
Now we will find the roots of the equation we get;

`7x^2-21x-4x+12=0\\\\7x(x-4)-4(x-4)=0\\\\(7x-4)(x-3)=0`

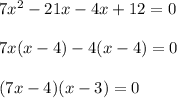
Now we will solve separately to find the value of x we get;

`7x-4=0 \ \ \ Or \ \ \ \ x-3=0\\\\7x=4 \ \ \ \ \ Or \ \ \ \ x=3\\\\x=(4)/(7)\ \ \ \ \ \ Or \ \ \ \ x=3`

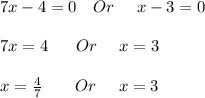
Now we get 2 values 1 in fraction and 1 integer but given the two numbers are positive integer hence we will discard the fraction value we get;

Larger number =
`x=3`

Smaller number =
`x-1=3-1=2`

Hence the two integers are 2 and 3.

Answer 2

2 and 3

Explanation:

A positive integer is 1 less than another.

If the sum of the reciprocal of the smaller and twice the reciprocal of the larger is
`(7)/(6)`

Question asked:

Then find the two integers.

Solution:

Let a positive integer is
`x`

Then another positive integer will be =
`x-1`

According to question,

Sum of the reciprocal of the smaller and twice the reciprocal of the larger is
`(7)/(6)`

Reciprocal of the smaller =
`(1)/(x-1)`

Twice the reciprocal of the larger =
`2*(1)/(x)=(2)/(x)`

Now, equation will be:-

`(1)/(x-1) +(2)/(x) =(7)/(6) \\ \\`

`Taking\ LCM\ of\ x\ and\ x-1,\ we\ get,\ x(x-1)`

`(x+2(x-1))/(x(x-1)) =(7)/(6) \\\\ (x+2x-2)/(x^(2) -x) =(7)/(6) \\\\ (3x-2)/(x^(2)-x ) =(7)/(6)`

By cross multiplication:

`6(3x-2)=7(x^(2) -x)\\18x-12=7x^(2) -7x`

Adding both sides by
`7x`

`25x-12=7x^(2) \ or\\7x^(2) -25x+12=0\\`

`7x^(2) -21x-4x+12=0\\`

`Taking\ common\\7x(x-3)-4(x-3)=0\\7x-4=0,x-3=0\\7x=4,x=3\\x=(4)/(7) ,x=3`

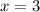
As we know that integer can never be a fraction but a whole number, hence
`x=3`, the 1 integer and the other will be
`x-1` = 3 - 1 = 2

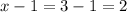
Therefore, two integers are 2 and 3.