Question

For each level of precision, find the required sample size to estimate the mean starting salary for a new CPA with 95 percent confidence, assuming a population standard deviation of $7,500 (same as last year).

Required: (Round your answers UP to the nearest integer.)

(a) E = $2,000

Sample size ??????
(b) E = $1,000

Sample size ????
(c) E = $500

Answer 1

(a) Margin of error ( E) = $2,000 , n = 54

(b) Margin of error ( E) = $1,000 , n = 216

(c) Margin of error ( E) = $500 , n= 864

Explanation:

Given -

Standard deviation
`\sigma` = $7,500

`\alpha` = 1 - confidence interval = 1 - .95 = .05

`Z_{(\alpha)/(2)}` =
`Z_{(.05)/(2)}` = 1.96

let sample size is n

(a) Margin of error ( E) = $2,000

Margin of error ( E) =
`Z_{(\alpha)/(2)}(\sigma)/(√(n))`

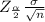
E =
`Z_{(.05)/(2)}(7500)/(√(n))`

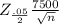
Squaring both side

`E^(2) = 1.96^(2)*(7500^(2))/(n)`

`n =(1.96^(2))/(2000^(2)) * 7500^(2)`

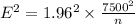
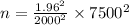
n = 54.0225

n = 54 ( approximately)

(b) Margin of error ( E) = $1,000

E =
`Z_{(\alpha)/(2)}(\sigma)/(√(n))`

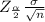
1000 =
`Z_{(.05)/(2)}(7500)/(√(n))`

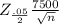
Squaring both side

`1000^(2) = 1.96^(2)*(7500^(2))/(n)`

`n =(1.96^(2))/(1000^(2)) * 7500^(2)`

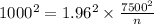
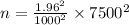
n = 216

(c) Margin of error ( E) = $500

E =
`Z_{(\alpha)/(2)}(\sigma)/(√(n))`

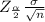
500 =
`Z_{(.05)/(2)}(7500)/(√(n))`

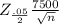
Squaring both side

`500^(2) = 1.96^(2)*(7500^(2))/(n)`

`n =(1.96^(2))/(500^(2)) * 7500^(2)`

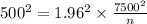
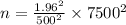
n = 864