Answer:
13.86 ft/sec
Explanation:
If we let x = distance batter has run at time t and D = distance from second base to the batter at time t, then we know
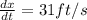 and we want
and we want
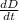 when he is halfway (at x = 45).
when he is halfway (at x = 45).
Using Pythagoras theorem

When x=45

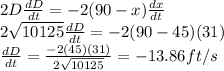
Thus, when the batter is halfway to first base, the distance between second base and the batter is decreasing at the rate of about 13.86 ft/sec.