Question

Using 0.500 g of nichrome, you are asked to fabricate a wire with uniform cross-section. The resistance of the wire is 0.673 Ω. The nichrome has a resistivity of 1.00 10^-6 Ω · m and a density of 8.31 10^3 kg/m^3.

a. What length of wire do you end up with?
b. What is the radius of the wire?

Answer 1

Step-by-step explanation:

Given that,

Mass of Nichrome, m = 0.5 g

The resistance of the wire, R = 0.673 ohms

Resistivity of the nichrome wire,
`\rho=10^(-6)\ \Omega -m`

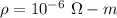
Density,
`d=8.31* 10^3\ kg/m^3`

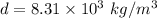
(A) The length of the wire is given by using the definition of resistance as :

Volume,

`V=A* l\\\\A=(V)/(l)\\\\Since, V=(m)/(d)\\\\V=(m)/(d)\\\\V=(0.5* 10^(-3))/(8.31* 10^3)\\\\V=6.01* 10^(-8)\ m^3`

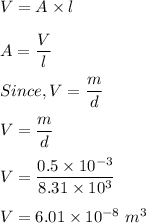
Area,

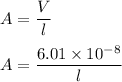`A=(V)/(l)\\\\A=(6.01* 10^(-8))/(l)`....(1)

`R=\rho (l)/(A)\\\\l=(RA)/(\rho)\\\\l=(0.673* 6.01* 10^(-8))/(l* 10^(-6))\\\\l=0.201\ m`

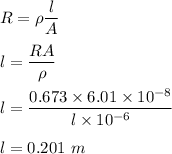
(b) Equation (1) becomes :

`A=(6.01* 10^(-8))/(l)\\\\A=(6.01* 10^(-8))/(0.201)\\\\\pi r^2=3* 10^(-7)\\\\r=\sqrt{(3* 10^(-7))/(\pi)} \\\\r=3.09* 10^(-4)\ m`

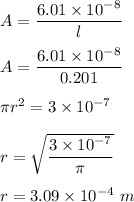
Hence, this is the required solution.