Question

Coaxial Cable A has twice the length, twice the radius of the inner solid conductor, and twice the radius of the outer cylindrical conducting shell of coaxial Cable B. What is the ratio of the inductance of Cable A to that of Cable BA) 4 ln 2B) 2C) 4 ln 4D) 2 ln 2E) 2 ln 4

Answer 1

Answer:2

Step-by-step explanation:

Given

Cable has twice the length of cable B

and twice the radius(both inner and outer) of cable B

Inductance is given by

`L=l* (\mu )/(2\pi )* \ln((R)/(r))`

Where l=length

r=inner radius

R=outer radius

`\mu`=Permeability of inner cylinder

suppose
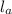`l_a` and
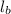`l_b` be the length of cable A and B

so
`l_a=2l_b`

`L_a=2l_b* (\mu )/(2\pi )* \ln((2R)/(2r))`

`L_a=2l_b* (\mu )/(2\pi )* \ln((R)/(r))---1`

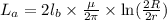
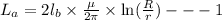
for wire B

`L_b=l_b* (\mu )/(2\pi )* \ln((R)/(r))---2`

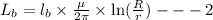
divide 1 and 2 we get

`(L_a)/(L_b)=2`