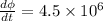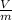Question

Suppose an air-gap capacitor has circular plates of radius R = 3.2 cm and separation d = 1.8 mm. A 91.0-Hz emf, ε=ε0cos(ωt) , is applied to the capacitor. The maximum displacement current is 40μA. Determine (a) the maximum conduction current I, (b) the value of ε0, (c) the maximum value of (dφe/dt) between the plates.

Answer 1

(a) The maximum conduction current is
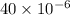`40 * 10^(-6)` A

(b) Value of
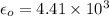`\epsilon _(o) = 4.41 * 10^(3)` V

(c) Maximum value of
`(d\phi)/(dt) = 4.5 * 10^(6)`
`(V)/(m)`

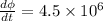
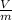
Step-by-step explanation:

Given:

Radius of circular plates
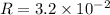`R = 3.2 * 10^(-2)` m

Separation between plates
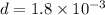`d = 1.8 * 10^(-3)` m

Frequency
`f = 91` Hz

Maximum displacement current
`I_(d) = 40 * 10^(-6)` A

(a)

Displacement current is equal to the conduction current so we write,

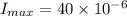`I _(max) = 40 * 10^(-6)` A

(b)

From the formula of displacement current,

`I _(d) = (\omega \epsilon _(o) \mu_(o) \pi r^(2) )/(d)`

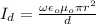
Where
`\mu _(o) = 8.85 * 10^(-12)`,
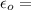`\epsilon _(o) =` peak value of emf,
`\omega = 2\pi f`

`\epsilon _(o) = (I_(d) d)/(2\pi f * \mu_(o) * \pi r^(2) )`

`\epsilon _(o) = (40 * 10^(-6) * 1.8 * 10^(-3) )/(6.28 * 91 * 8.85 * 10^(-12) * 3.14 (3.2 * 10^(-2) )^(2) )`

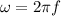
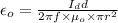
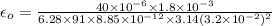
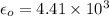`\epsilon _(o) = 4.41 * 10^(3)` V

(c)

From another formula of displacement current,

`I_(d) = \mu_(o) (d\phi)/(dt)`

Where
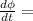`(d\phi)/(dt) =` change in flux

`(d\phi)/(dt) = (40* 10^(-6) )/(8.85 * 10^(-12) )`

`(d\phi)/(dt) = 4.5 * 10^(6)`
`(V)/(m)`

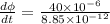
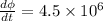
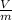
Therefore, the maximum conduction current is
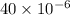`40 * 10^(-6)` A and value of

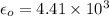`\epsilon _(o) = 4.41 * 10^(3)` V and maximum value of
`(d\phi)/(dt) = 4.5 * 10^(6)`
`(V)/(m)`