Question

Confidence Interval Mistakes and Misunderstandings—Suppose that 500 randomly selected recent graduates of a university were asked to rate the school’s academic advising services on a scale from 1 to 10. The sample mean rating was found to be 8.6. Assume that the population standard deviation is known to be 2.2

A.) Someone computes the 95% confidence interval for the average satisfaction score as 8.6 ± 1.96(2.2). What is the mistake of this student?

B.) After correcting the mistake in part (A), the student states "I am 95% confident that the sample mean rating falls between 8.4 and 8.8." What is wrong with this statement?

C.) The student quickly realizes the mistake made in part (B) and now says "The probability that the true mean rating is between 8.4 and 8.8 is 95%." What misinterpretation is the student making now?

D.) Finally, to defend the use of the Normal distribution to calculate the confidence interval the student says, "Because the sample size is quite large, the population of alumni ratings will be approximately Normal." Correct this misunderstanding.

Answer 1

The correct 95% confidence interval is (8.4, 8.8).

Explanation:

The information provided is:

`n=500\\\bar x=8.6\\\sigma=2.2`

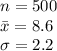
(a)

The (1 - α)% confidence interval for population mean (μ) is:

`CI=\bar x\pm z_(\alpha/2)* (\sigma)/(√(n))`

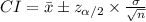
The 95% confidence interval for the average satisfaction score is computed as:

8.6 ± 1.96 (2.2)

This confidence interval is incorrect.

Because the critical value is multiplied directly by the standard deviation.

The correct interval is:

`8.6\pm 1.96 ((2.2)/(√(500)))=8.6\pm 0.20=(8.4,\ 8.6)`

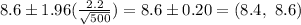
(b)

The (1 - α)% confidence interval for the parameter implies that there is (1 - α)% confidence or certainty that the true parameter value is contained in the interval.

The 95% confidence interval for the mean rating, (8.4, 8.8) implies that the true there is a 95% confidence that the true parameter value is contained in this interval.

The mistake is that the student concluded that the sample mean is contained in between the interval. This is incorrect because the population is predicted to be contained in the interval.

(c)

The (1 - α)% confidence interval for population parameter implies that there is a (1 - α) probability that the true value of the parameter is included in the interval.

The 95% confidence interval for the mean rating, (8.4, 8.8) implies that the true mean satisfaction score is contained between 8.4 and 8.8 with probability 0.95 or 95%.

Thus, the students is not making any misinterpretation.

(d)

According to the Central Limit Theorem if we have a population with mean μ and standard deviation σ and we take appropriately huge random samples (n ≥ 30) from the population with replacement, then the distribution of the sample mean will be approximately normally distributed.

In this case the sample size is,

n = 500 > 30

Thus, a Normal distribution can be applied to approximate the distribution of the alumni ratings.