Question

A metal ring is oriented with the plane of its area perpendicular to a spatially uniform magnetic field that increases at a steady rate. After the radius of the ring is doubled, while the rate of increase of the field is cut in half, the emf induced in the ring a. increases by a factor of 2. b. decreases by a factor of 2.c. remains the same. d. increases by a factor of 4.

Answer 1

The emf induced in the ring increases by a factor of 2.

Step-by-step explanation:

The formula of induced emf is given by :

`\epsilon=-(d\phi)/(dt)\\\\\epsilon=-(d(BA))/(dt)\\\\\epsilon=-\pi r^2(dB)/(dt)`

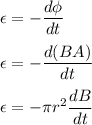
If the the radius of the ring is doubled, while the rate of increase of the field is cut in half.

New emf is given by :

`\epsilon=-\pi r'^2(dB')/(dt)\\\\\epsilon'=-\pi (2r)^2(dB)/(2dt)\\\\\epsilon'=-2\pi r^2(dB)/(dt)\\\\\epsilon'=-2* \epsilon`

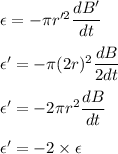
So, the emf induced in the ring increases by a factor of 2.