Question

A catering service offers 10 appetizers, 4 main courses, and 6 desserts. A costumer is to select 9 appetizers, 2 main courses, and 5 desserts for a banquet. In how many ways can this be done?

Answer 1

720 ways.

Explanation:

Given:

A catering service offers 10 appetizers, 4 main courses, and 6 desserts.

A costumer is to select 9 appetizers, 2 main courses, and 5 desserts for a banquet.

Question asked:

In how many ways can this be done ?

Solution:

By applying combination's formula:-

`^(n) C_(r)=(n!)/((n-r)!\ r!)`

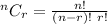
A costumer can choose 9 appetizers out of 10 in =

`^(10) C_(9)=(10!)/((10-9)!\ 9!)=(10*9!)/(1!*9!) ,\ 9!\ canceled\ by\ 9! =10\ ways`

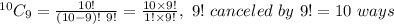
A costumer can choose 2 main courses out of 4 in =

`^(4) C_(2)=(4!)/((4-2)!\ 2!)=(4*3*2!)/(2!*2!) =(12)/(1*1) =12\ ways`

A costumer can choose 5 desserts out of 6 in =

`^(6) C_(5)=(6!)/((6-5)!\ 5!)=(6*5!)/(1!*5!) =(6)/(1) =6\ ways`

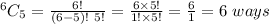
Total number of ways =
`10*12*6=720\ ways`

Therefore, A costumer can select 9 appetizers, 2 main courses, and 5 desserts for a banquet in 720 ways.