Question

A report on electronic monitoring and surveillance summarized a survey of 306 U.S. businesses. The report stated that 93 of the 306 businesses had fired workers for misuse of the Internet. Assume that this sample is representative of businesses in the United States. (a) Estimate the proportion of all businesses in the U.S. that have fired workers for misuse of the Internet. (Round your answer to three decimal places.) What statistic did you use? sample size sample variance sample proportion sample mean sample standard deviation (b) Use the sample data to estimate the standard error of p. (Round your answer to three decimal places.) (c) Calculate the margin of error associated with the estimate in part (a). (Hint: See Example 9.3. Round your answer to three decimal places.) Interpret the margin of error associated with the estimate in part (a). (Hint: See Example 9.3.) It is unlikely that the estimate in part (a) differs from the true population proportion by less than the value calculated above. It is unlikely that the estimate in part (a) differs from the true population proportion by more than the value calculated above. It is impossible that the estimate in part (a) differs from the true population proportion by more than the value calculated above It is impossible that the estimate in part (a) differs from the true population proportion by less than the value calculated above. It is likely that the estimate in part (a) differs from the true population proportion by the value calculated above

Answer 1

Explanation:

Hello!

Variable of interest is

X: Number of businesses that had fired workers for misuse of the internet out of 306 businesses.

The parameter of interest is the population proportion of businesses that had fired workers for misuse of the internet, symbolized p.

a)

The estimator of the population proportion is the sample proportion. You can calculate the sample proportion by dividing the number of successes by the sample size:

p'= x/n= 93/306≅ 0.30

b)

Considering the approximate distribution of the sample proportion:

p'≈N(p;
`(p(1-p))/(n)`)

The variance of the distribution is
`(p(1-p))/(n)`, and its estimation is
`(p'(1-p'))/(n)`

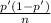
The estimation of the standard error is then
`\sqrt{(p'(1-p'))/(n) } = \sqrt{(0.30*0.70)/(306) }= 0.026`

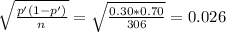
c)

The CI for the population proportion is

p' ±
`Z_(1-\alpha /2) * \sqrt{((p'(1-p')))/(n) }`

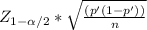
Where
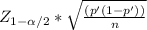`Z_(1-\alpha /2) * \sqrt{((p'(1-p')))/(n) }` represents the margin of error of the interval.

To calculate it you need a confidence level for the interval.

Let's say for example that you are using a level of 1 - α= 90%, then the value of Z for the margin of error is
`Z_(1-\alpha /2)= Z_(0.95)= 1.648`

`Z_(1-\alpha /2) * \sqrt{((p'(1-p')))/(n) }= 1.648*\sqrt{(0.3*0.7)/(306) } = 0.04`

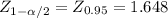
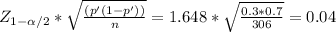
Interpret the margin of error associated with the estimate in part (a).

It is unlikely that the estimate in part (a) differs from the true population proportion by less than the value calculated above.

It is unlikely that the estimate in part (a) differs from the true population proportion by more than the value calculated above.

It is impossible that the estimate in part (a) differs from the true population proportion by more than the value calculated above

It is impossible that the estimate in part (a) differs from the true population proportion by less than the value calculated above.

It is likely that the estimate in part (a) differs from the true population proportion by the value calculated above

I hope it helps!