Answer:
The capacitance of a spherical capacitor can be give by

Step-by-step explanation:
Let Q = Magnitude of the charge on the spherical conductor
a = Radius of the smaller sphere
b = Radius of the larger sphere
According to Gauss' law,
![E [4\pi r^(2) ] = (Q)/(\epsilon_(0) )](https://img.qammunity.org/2021/formulas/physics/college/ns50oafxu9602y8qp1sl5n6wqh7q2q98v6.png)
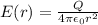
The electric potential between the spherical conductor is given by :
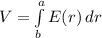

![V = (Q)/(4\pi \epsilon_(0) )[(1)/(a) - (1)/(b) ]\\V = (Q)/(4\pi \epsilon_(0) )[(b-a)/(ab) ]](https://img.qammunity.org/2021/formulas/physics/college/l5zc8nzki76liac7iidinz59d2jte2qprp.png)
But
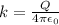
![V = kQ[(b-a)/(ab) ]](https://img.qammunity.org/2021/formulas/physics/college/pen18z0ovc4tii44xj207stqpn1qf20wt9.png)
The capacitance of the spherical capacitor can be given by
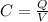
![C = (Q)/( kQ[(b-a)/(ab) ]) \\C = (ab)/(k(b-a))](https://img.qammunity.org/2021/formulas/physics/college/nv1xqowwditx5we5p5wbqos7s30ubu5nso.png)