Question

The Quality Control Department employs five technicians during the day shift. Listed below is the number of times each technician instructed the production foreman to shut down the manufacturing process last week.

Technician Shutdowns
Taylor 2
Hurley 1
Gupta 3
Rousche 5
Huang 4

a. How many samples, without replacement, of size two are possible?
b. Compute the mean of the sample means and compare it to the population mean.

Answer 1

a

The number is
`= 10`

b

The sample mean is = 3.2

The population mean is = 3

The sample mean is greater than population mean

Explanation:

From the question we can see that the number of technicians is
`n=5`

Generally we can obtain the number of sample without replacement of size two that is possible using this formula

`^n C_r`

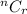
This denote Combination which is mathematically represented as

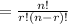`= (n!)/(r!(n-r)!)` where ! denotes factorial

So substituting 5 for n and 2 for r

No of samples without replacement of size 2
`= (5!)/(2!(5-2)!)`

`= 10`

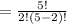
The sample mean of the 10 samples are shown on the first uploaded image

The population means is mathematically evaluated as
`(2+ 1+3 + 5+ 4)/(5) = 3`

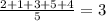
From the calculation on the on the table for sample mean and the population mean calculation we see that

the sample mean is greater than population mean

Answer 2

a. The possible samples is 10

b. The mean of the sample mean is 3 and the population mean is 3.

Both the sample mean and the population mean is the same.

Explanation:

The image attached show the step by step solution.