Question

The base of a merry-go-round spans an area of about 153.88 square meters What is the radius of

the merry-go-round?
Nysean says the radius of the merry-go-round is 14 meters. Do you agree or disagree? Explain.

Answer 1

Disagree

radius = 7 m

diameter = 14 m

Explanation:

Formula

`\sf Area\:of\:a\:circle=\pi r^2`

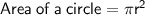
Given:

• area = 153.88 m²

Substitute given value into the formula and solve for r:

`\sf \implies \pi r^2=153.88`

`\sf \implies r^2=(153.88)/(\pi)`

`\sf \implies r=\sqrt{(153.88)/(\pi)}`

`\sf \implies r=6.998680253`

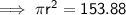
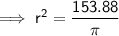
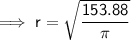
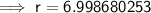
Therefore r ≈ 7 m

So I disagree with Nysean, as from my calculations, the approximate radius of the merry-go-round is 7 m.

Diameter = 2r

⇒ diameter of merry-go-round = 2 x 7 = 14m

So Nysean has actually given the approximate measure of the diameter rather than the radius.