Question

In 1996, the general social survey (which uses a method similar to simple random sampling) asked, "on the whole, do you think it should be the government's responsibility to provide decent housing for those who can't afford it?" for this question, 240 people said that it definitely should out of 1572 randomly selected people.

We will make a 90% confidence interval for ______ standard error.

a) 0.1527
b) 0.0091
c) 0.000082
d) We need to know the confidence level to compute this.

Answer 1

b) 0.0091

Explanation:

Hello!

The variable of interest is

X: Number of people that answered the social survey affirmatively out of 1572.

This variable has a binomial distribution.

The sample proportion is p'= 240/1572= 0.15

The distribution of the sample proportion (p') is

p'≈ N(p;
`(p(1-p))/(n)`)

The standard deviation of the distribution is
`\sqrt{(p(1-p))/(n) }`

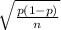
As you can see, the population proportion is present in the variance of the sampling distribution. To be able to estimate the population proportion using the sampling distribution, the variance must be estimated, so for the CI the standard error is
`\sqrt{(p'(1-p'))/(n) }`

`\sqrt{(p'(1-p'))/(n) }`=
`\sqrt{(0.1527(1-0.1527))/(1572) }= 0.00907`

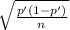
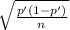The correct answer is b)

I hope this helps!