Question

g In a local university, 80% of the students live in the dormitories. A random sample of 80 university students is selected to participate ina particular study.What is the probability that the sample proportion (the proportion living in the dormitories) is between 0.70 and 0.85

Answer 1

0.8554 is the probability that the proportion of students living in dormitories is between 0.70 and 0.85

Step-by-step explanation:

We are given the following in the question:

Proportion of students who live in dormitories = 80%

`p= 0.80`

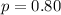
Sample size, n = 80

Thus, the number of students follow a binomial distribution,

We use normal approximation to the binomial distribution to find the probability.

Parameters of Normal distribution:

`\mu = np = 80* 0.80 = 64\\\sigma = √(np(1-p)) = √(80(0.80)(1-0.80)) = 3.58`

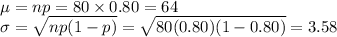
We have to find the probability that the sample proportion (the proportion living in the dormitories) is between 0.70 and 0.85.

`P(0.70\leq p \leq 0.85)\\\\=P(0.70(80)\leq x \leq0.85(80))\\\\=P(56 \leq x \leq 68) \\\\= P(\displaystyle(56 - 64)/(3.58) \leq z \leq \displaystyle(68-64)/(3.58))\\\\ = P(-2.2346 \leq z \leq 1.1173)\\\\= P(z \leq 1.1173) - P(z < -2.2346)\\\\= 0.8681 - 0.0127 = 0.8554`

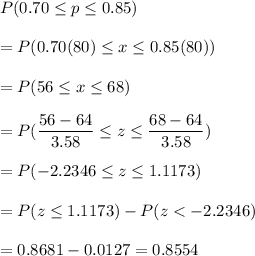
Thus, 0.8554 is the probability that the proportion of students living in dormitories is between 0.70 and 0.85