
 Let the women's height be AE and distance between the women and tower be AC.
Let the women's height be AE and distance between the women and tower be AC.
Also let the height of tower be BC.
 Now, clearly it is forming a triangle.
Now, clearly it is forming a triangle.
So, in triangle ABC,

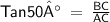

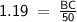

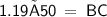

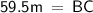
 Hence, BC = 59.5m
Hence, BC = 59.5m
So, BD(total height of the tower)
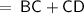
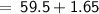
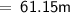
Therefore, total height of the tower =
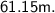
________________________________
Hope it helps you:)