Answer:
We conclude that the second graders who participate in sports does not have a higher mean dexterity score.
Explanation:
We are given that a random sample of 37 second graders who participated in sports had manual dexterity scores with mean 32.19 and standard deviation 4.34. An independent sample of 37 second graders who did not participate in sports had manual dexterity scores with mean 31.68 and standard deviation 4.56.
We have to conduct a hypothesis test to see whether sufficient evidence exists to indicate that second graders who participate in sports have a higher mean dexterity score.
Let
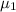 = population mean dexterity scores for second graders who participated in sports
= population mean dexterity scores for second graders who participated in sports
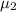 = population mean dexterity scores for second graders who did not participated in sports
= population mean dexterity scores for second graders who did not participated in sports
SO, Null Hypothesis,
 :
:
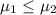 or
or
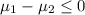 {means that the second graders who participate in sports have less than or equal mean dexterity score}
{means that the second graders who participate in sports have less than or equal mean dexterity score}
Alternate Hypothesis,
 :
:
 or
or
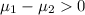 {means that the second graders who participate in sports have a higher mean dexterity score}
{means that the second graders who participate in sports have a higher mean dexterity score}
The test statistics that will be used here is Two-sample t test statistics as we don't know about the population standard deviations;
T.S. =
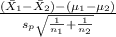 ~
~
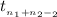
where,
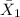 = sample mean dexterity scores for 37 second graders who participated in sports = 32.19
= sample mean dexterity scores for 37 second graders who participated in sports = 32.19
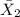 = sample mean dexterity scores for 37 second graders who did not participated in sports = 31.68
= sample mean dexterity scores for 37 second graders who did not participated in sports = 31.68
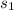 = standard deviation for 37 second graders who participated in sports = 4.34
= standard deviation for 37 second graders who participated in sports = 4.34
 = standard deviation for 37 second graders who did not participated in sports = 4.56
= standard deviation for 37 second graders who did not participated in sports = 4.56
 = sample size for second graders who participated in sports = 37
= sample size for second graders who participated in sports = 37
 = sample size for second graders who did not participated in sports = 37
= sample size for second graders who did not participated in sports = 37
Here,
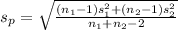 =
=
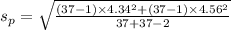 = 4.45
= 4.45
So, test statistics =
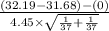 ~
~
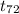
= 0.493
So, at 0.05 level of significance, the t table gives critical value of 1.6684 at 72 degree of freedom for one-tailed test. Since our test statistics is less than the critical value of t so we have insufficient evidence to reject null hypothesis as it will not fall in the rejection region.
Therefore, we conclude that the second graders who participate in sports does not have a higher mean dexterity score.