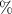Answer:
The percent of men heights between 64 and 78 inches = 96.22
Explanation:
Given -
Mean height
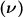 = 69.0
= 69.0
Standard deviation
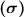 = 2.8
= 2.8
Let X be the height of american man
The percent of men heights between 64 and 78 inches =
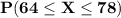 =
=
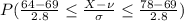
=
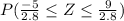 Put [
Put [
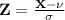 ]
]
=
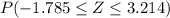 Using z table
Using z table
= 0.9993 - .0370
= .9622
= 96.22