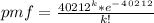Question

Suppose that trees are distributed in a forest according to a two-dimensional Poisson process with lambda the expected number of trees per acre given by 80.

a. What is the probability that in a certain quarter acre plot there will be at most 16 trees?
b. If the forest covers 85,000 acres, what is the expected number of trees in the forest?
c. Suppose you select a point in the forest and construct a circle of radius 0.1 mile. Let X the number of trees within that circular region. What is the pmf of X?

Answer 1

a) 372640 / e^80

b) E(X) = 6,800,000 trees

c)
`pmf = (40212^k * e^-^4^0^2^1^2)/(k!)`

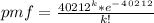
Explanation:

Given:-

- The parameter (λ) = 80

- The random variable X:

X ~ Po ( 80 )

Solution:-

a) P ( X ≤ 16 ):-

- We will use the pmf function for the poisson distribution to evaluate the asled probability as follows:

`P(X\leq 16) = \sum _(n=0)^(16)\:(\left(λ\right)^n\cdot \left(e^(-λ)\right))/(n!)\\\\P(X\leq 16) = \sum _(n=0)^(16)\:(\left(80\right)^n\cdot \left(e^(-80)\right))/(n!)\\\\P(X\leq 16) = (372640)/(e^(80))`

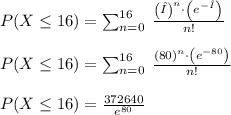
b) If the forest covers 85,000 acres, what is the expected number of trees in the forest?

- From given data it is known that:

per acre : E(X) = 80

85,000 acres : E(X) = 85,000*(80)

= 6,800,000 trees per 85,000 acres

c) Suppose you select a point in the forest and construct a circle of radius 0.1 mile. Let X the number of trees within that circular region. What is the pmf of X?

Solution:-

- The value of the parameter ( λ ) is given for "acres". We will first convert acres to square miles.

1 acre = 0.0015625 miles^2

- So,

λ = 80 trees / 0.0015625 miles^2

λ = 51,200 trees / miles^2

- The area covered by the circular region is denoted by its radius r = 0.5 miles.

A_circle = π*r^2

= π*(0.5)^2

= 0.78539 miles^2

- Using direct proportions we have:

1 square mile --------- > 51,200 trees

0.78539 square mile ---> x trees

=====================================

x = 51,200*(0.78539) = 40,212 trees

=====================================

- The random variable (X) follows the Poisson distribution with parameter ( λ = 40,212 trees / miles ) with pmf:

`pmf = (40212^k * e^-^4^0^2^1^2)/(k!)`